Research

This is a brief summary of some of the things I work on. You can find my latest publications with some tl;dr’s here.

Foundations and Applications of Emergence

There is a lot to learn about emergence and complex systems, and everyone uses their own language. My approach is:

• Algebraic
  • Algebra comes from the Arabic “al-jabr” which means something like ‘bringing parts together’. That makes it a good language for talking about complex systems.
• Computational
  • Everything I do gets implemented in code at one point.
• Compositional
  • I like thinking about hierarchies, categories, and openness

A lot of this comes together in this paper, which presents a unified perspective on `higher-order’ interactions in complex systems. It turns out that across the sciences, interactions among parts of a system can be described by a common mathematical structure, based on a certain compositional/algebraic view of the world. This turns out to be very useful! Stay tuned…

Information theory and Biology

Information theory is a natural bridge between the physical and living systems. I am specifically interested in some extensions of Shannon’s theory, such as information decomposition, higher-order information theory, and quantum information. I’ve applied this to brains, genes, magnets, worms, qubits, Bach’s chorales, and more…

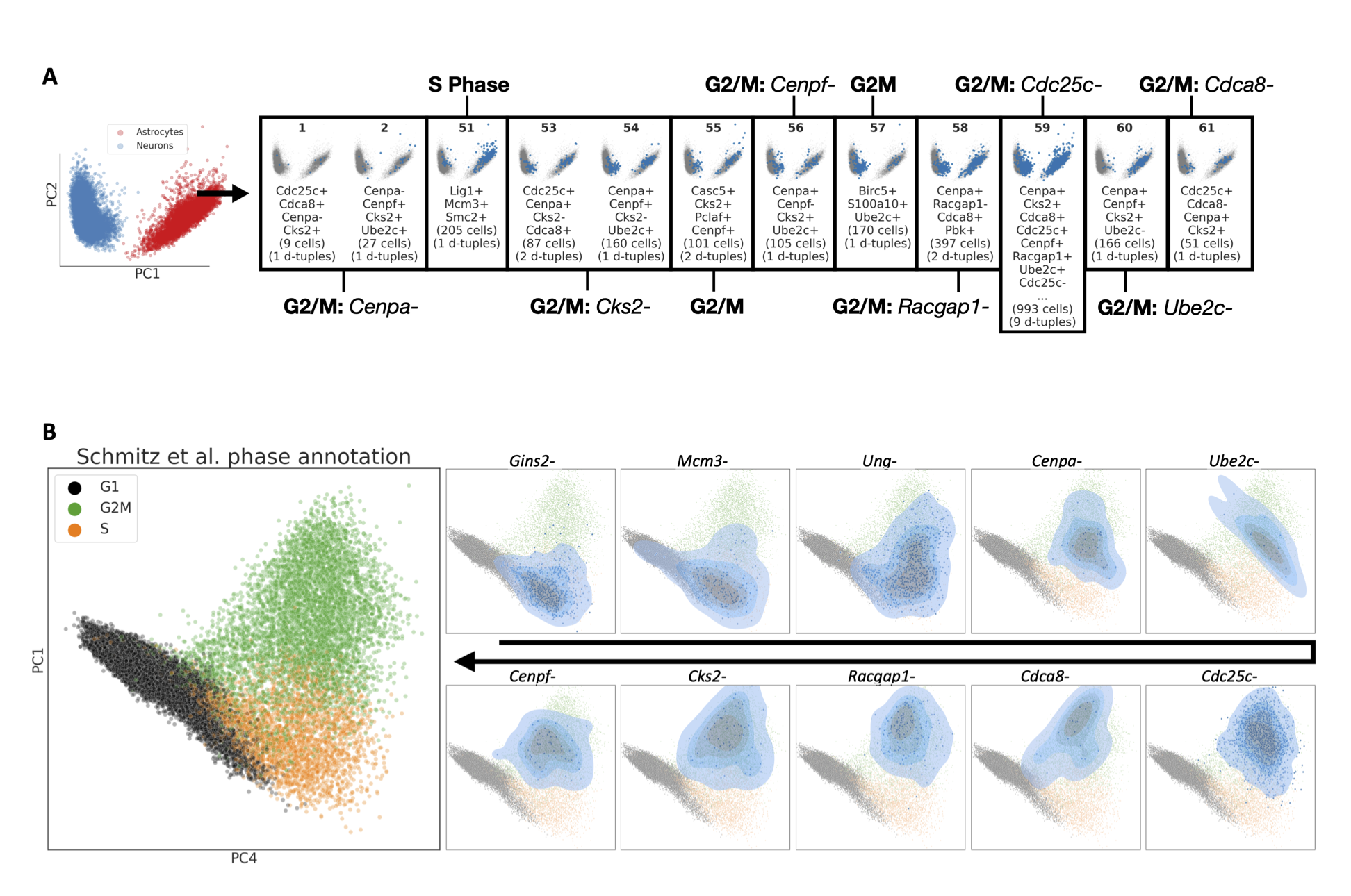
Stator: Higher-order genetic interactions and cells states

I developed a software package called Stator to use higher-order interactions among RNA molecules to identify new cell states hiding in single-cell transcriptomic data sets. Here, we used this to find future fates of embryonic neurons, and liver cancer states that are prognostic of patient survival.