Geometric correlations
This is the first post in a series on dualities in statistics and machine learning. It's a good start because it's a simple and short example of the kind of dualities I like. It's not particularly useful, but shows how a seemingly arbitrary definition arises very naturally from a more fundamental concept, like a geometrical structure. Here we will show the geometric interpretation of the correlation between two variables.
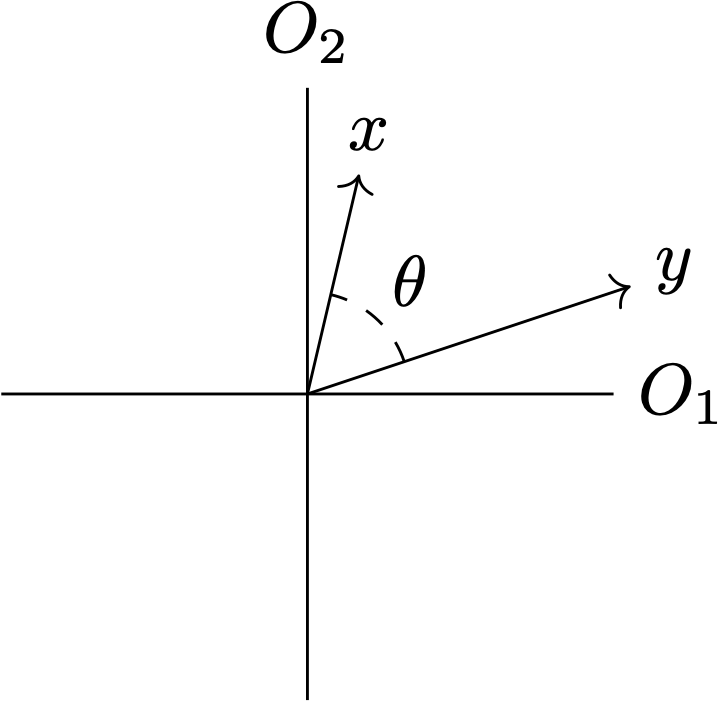
Where $\theta = \cos^{-1}{\rho_{xy}}$ and $O_i$ is the $i$th observation.
The sample correlation example is famous, and reproduced a lot, but I can not find any reference for the second case. I'm sure I'm missing some nuance and somebody has thought of this before, any suggestions?
tags:
Sample correlation as a cosine
Suppose you make N observations of two discrete variables $x$ and $y$. These are now just two lists of numbers, so we might as well treat them as vectors in $\mathbb{R}^N$ (not unlike a Gaussian process). Let's put the usual Euclidean inner product on this space, and define $$ \langle x, y \rangle := \sum_i^N x_i y_i $$ Which is a good inner product because it's obviously symmetric, linear, and positive definite. It thus also induces a norm $|x| = \sqrt{\langle x, x \rangle}$, which allows us to relate this inner product to the angle $\theta$ between the vectors in $\mathbb{R}^N$ in the usual way as $$ \langle x, y \rangle = \cos(\theta) |x| |y| $$ This gives us a nice way to compare how similar two variables are: just calculate the angle between them! The smaller this angle, the more similar they are in each observation. We might want to centre our observations around zero to get rid of any gauge effects: $$ \begin{align} \langle x-\mu_x, y-\mu_y \rangle &= \cos(\theta) |x-\mu_x| |y-\mu_y|\\ &= \cos(\theta) \langle x-\mu_x, x-\mu_x \rangle \langle y-\mu_y, y-\mu_y \rangle\\ \text{Or equivalently:}\\ \implies \cos(\theta) &= \frac{\langle x-\mu_x, y-\mu_y \rangle}{\langle x-\mu_x, x-\mu_x \rangle \langle y-\mu_y, y-\mu_y \rangle}\\ &= \frac{\sum_i (x_i - \mu_x) (y_i - \mu_y)}{\sqrt{\sum_i (x_i - \mu_x)^2\sum_i (y_i - \mu_y)^2}} \end{align} $$ Which is exactly the Pearson correlation $\rho_{xy}$ of N samples. This gives a very natural interpretation of a correlation: it's the angle between the vectors of observations, perhaps the most fundamental way to talk about similarity of two points in a space:
Extending this to a whole population
Above, we have specifically looked at the correlation of samples: a finite list of paired observations. What about more general random variables? Can we identify an angle with the correlation as defined by: $$\rho_{XY} = \frac{\mathbb{E}[(X-\mu_X)(Y-\mu_Y)]}{\sqrt{\mathbb{E}[(X-\mu_X)^2]\mathbb{E}[(Y-\mu_Y)^2]}}$$ Well, following the same line of reasoning as before, it looks like we can associate a weighted inner product with this as follows (I'm not sure if it's a proper inner product, there might be issues with linearity. If that bothers you, let the following define a new bracket): $$\langle X, Y \rangle = \sum_{x, y} p(x, y) x y$$ Where the sum now goes over the whole state space of the system. Naively, let us also in this case write: $$\cos(\theta) = \frac{\langle x-\mu_x, y-\mu_y \rangle}{\sqrt{\langle x-\mu_x, x-\mu_x \rangle \langle y-\mu_y, y-\mu_y \rangle}}$$ This is a nice expression, since this looks a lot like the general definition of angles on a Riemannian manifold (Einstein summation implied): $$\cos{\theta} = \frac{g_{ij}X^i Y^j}{\sqrt{|g_{ij} X^i X^j| |g_{ij} Y^i Y^j|}} $$ Where the probability distribution plays the role of the metric tensor, and the centered data that of the tangent vectors. This again gives a cool interpretation of a correlation as an angle, but in a completely different space! Before, the sample correlation was an angle in a space where each dimension is an observation. For the whole population, the correlation is an angle in the state space of the system, endowed with a metric through the probability distribution.The sample correlation example is famous, and reproduced a lot, but I can not find any reference for the second case. I'm sure I'm missing some nuance and somebody has thought of this before, any suggestions?
dualities-in-statistics maths