Elementary Open Games as String diagrams
(This is an update on my Ethereum Protocol Fellowship. More updates can be found here ).
The Open Game engine compiles the DSL to Haskell. The DSL describes the externals (dangling wires) and internals (compositional structure) of an open game. Note that closed games are open games without dangling wires. The DSL is tasked with combining the sequential compositional and parallel/monoidal composition into a single linear script. To do so, it defines how each process depends on the outputs of the other processes. Note to self: this is extremely similar to how Nextflow links processes and infers trivial parallelisation in a pipeline.
To see if I understand the OG DSL well enough, I set myself the challenge to draw the introductory examples as string diagrams.
There are four kinds of games listed:
Decision Games
singleDecision
The game is defined as
singleDecisionReduced actionSpace payoffFunction = [opengame|
operation : dependentDecision "player1" (const actionSpace);
outputs : decisionPlayer1 ;
returns : payoffFunction decisionPlayer1 ;
|]
which from the external view looks like the following trivial game:
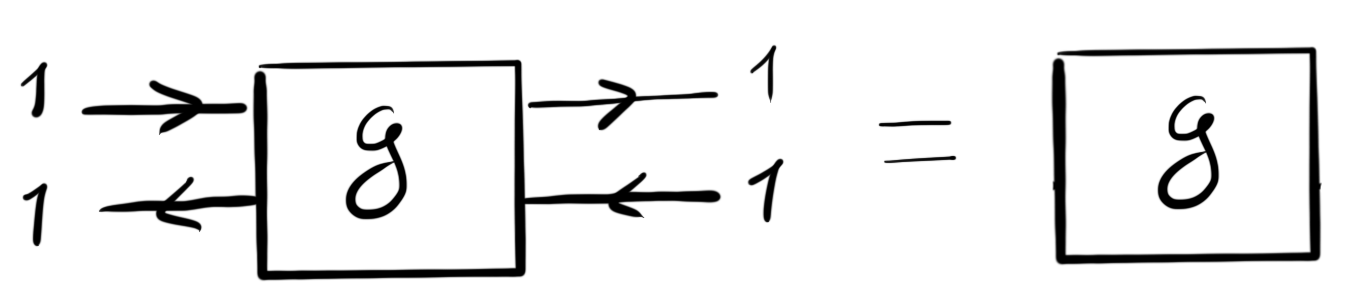
However, the internal view is more interesting (drawing dashed lines to show the boundary between the interior and the exterior):
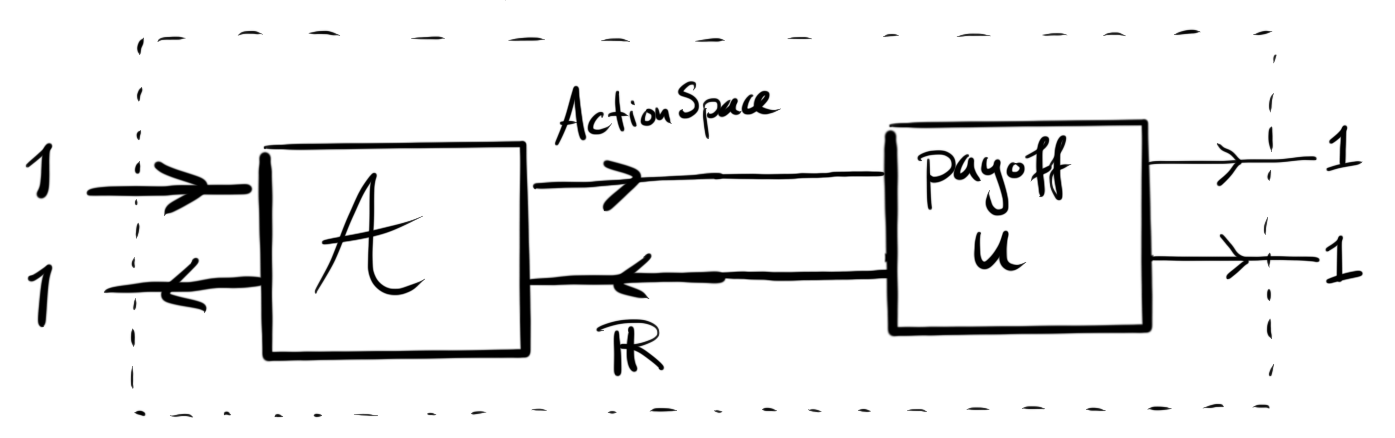
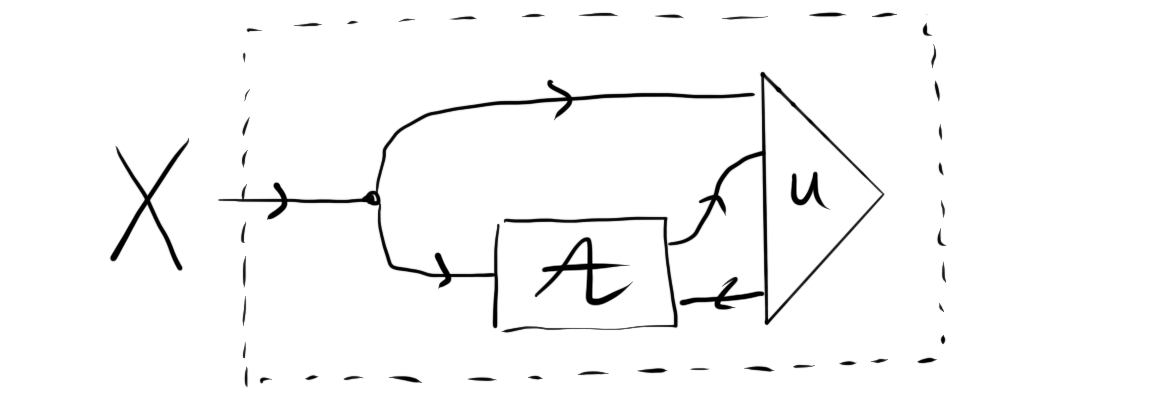
which in turn can be summarised as
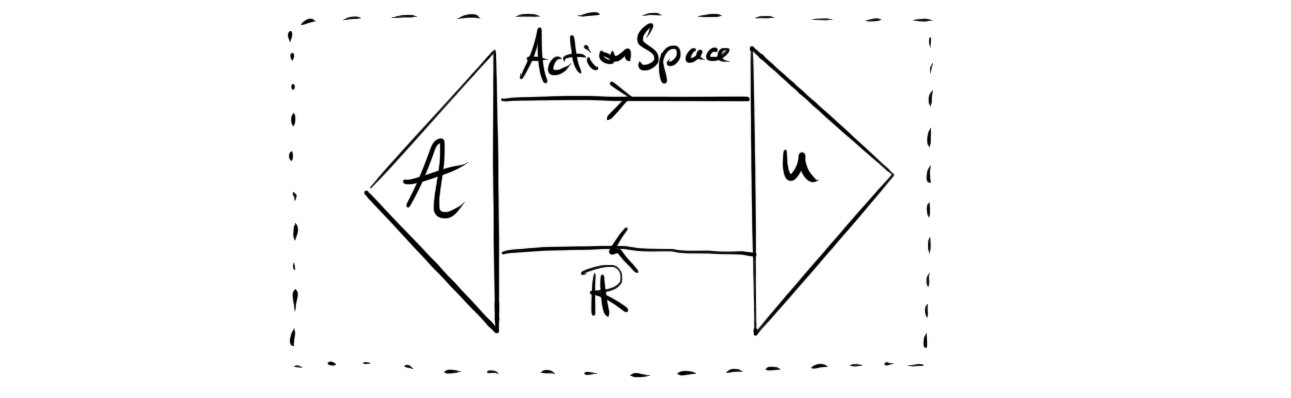
from which it can indeed be seen that it does not require a context.
singleDecisionPrior
The game is defined as
(Fabrizio kindly pointed out that this previously contained a typo, PR submitted here)
singleDecisionPriorReduced actionSpace payoffFunction = [opengame|
inputs : x ;
:----------------------------:
inputs : x ;
operation : dependentDecision "player1" (\x -> actionSpace);
outputs : decisionPlayer1 ;
returns : payoffFunction decisionPlayer1 x ;
|]
which from the external view looks like the following almost-trivial game:
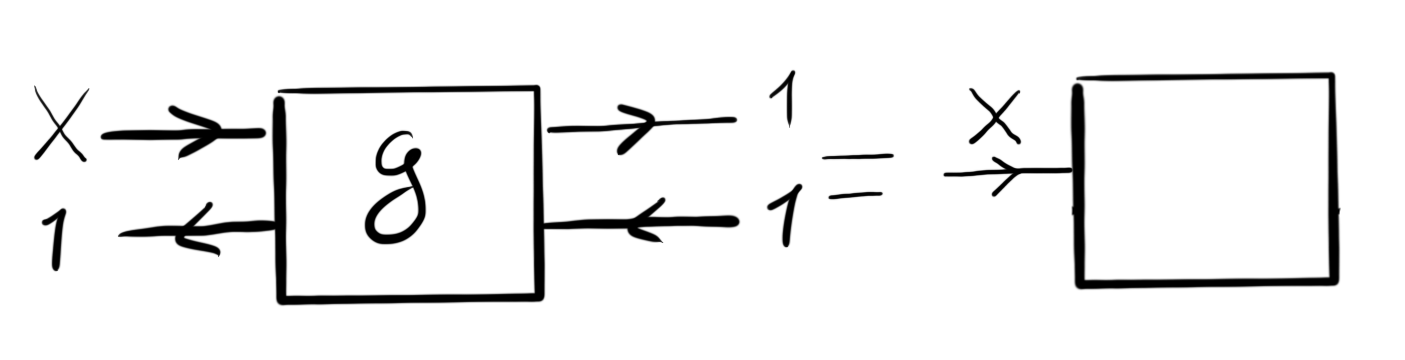
Again, the interior view is more interesting:
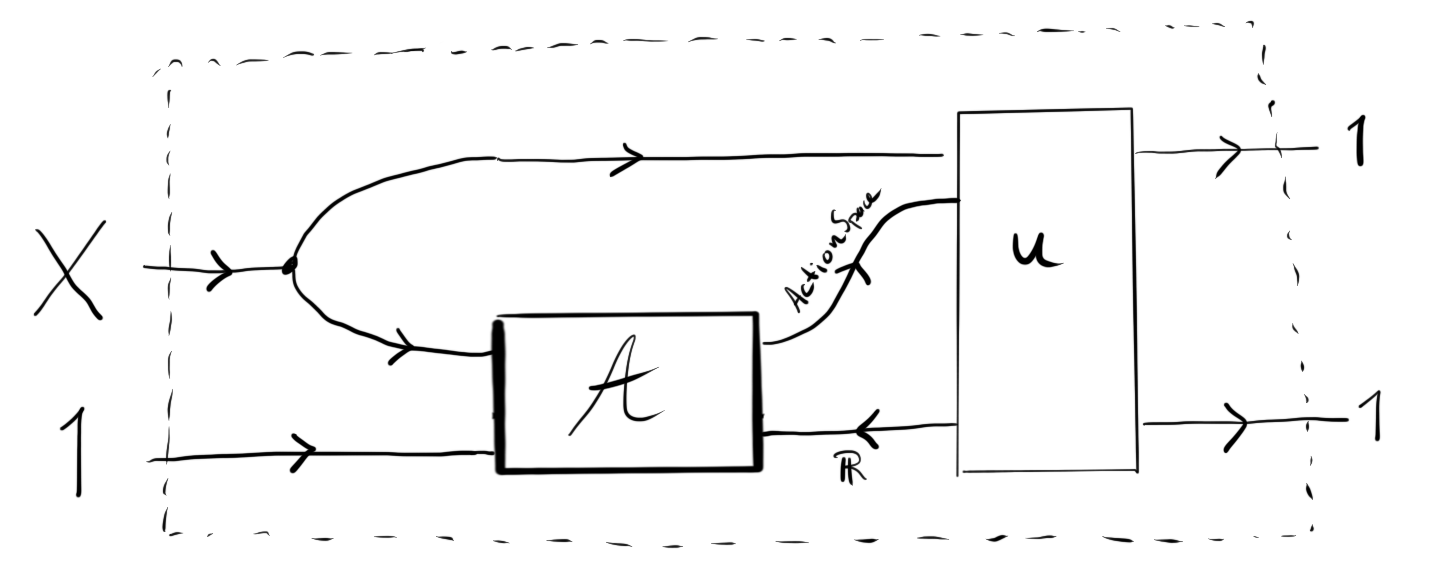
which is
singleDecStoch
The game is defined in two parts, that are sequentially composed. In verbose form:
stochasticEnv distribution = [opengame|
inputs : ;
feedback : ;
:----------------------------:
inputs : ;
feedback : ;
operation : nature distribution;
outputs : draw ;
returns : ;
:----------------------------:
outputs : draw ;
returns : ;
|]
singleDecStoch distribution actionSpace payoffFunction = [opengame|
inputs : ;
feedback : ;
:----------------------------:
inputs : ;
feedback : ;
operation : stochasticEnv distribution ;
outputs : draw ;
returns : ;
inputs : draw ;
feedback : ;
operation : singleDecisionPriorVerbose actionSpace payoffFunction;
outputs : ;
returns : ;
:----------------------------:
outputs : ;
returns : ;
|]
The game singleDecStoch is trivial from the external point of view, but has a nested internal structure as it includes the previous game (singleDecisionPrior) in the operation.
At the first level of nesting, it is a sequential composition of the game that draws a type $X$ from Nature, and the almost-trivial game $g’$ which receives an input of type $X$:
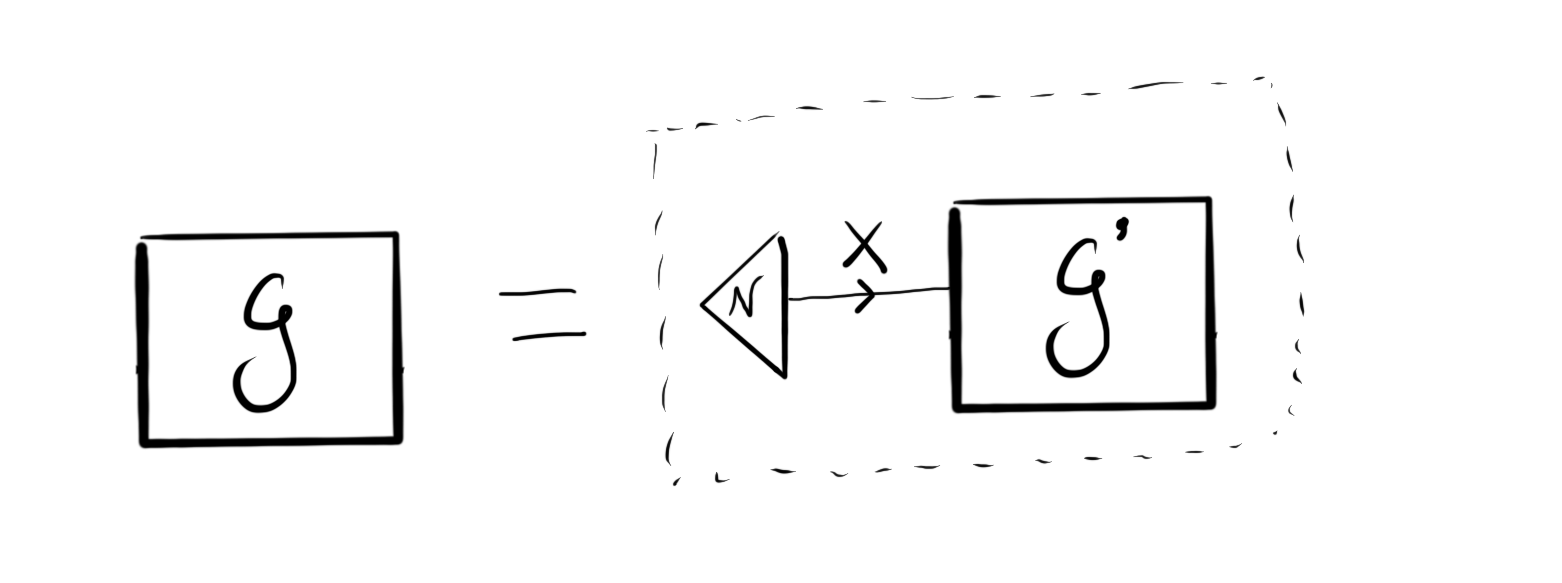
However, this game $g’$ is the game singleDecStoch from before. Substituting that yields
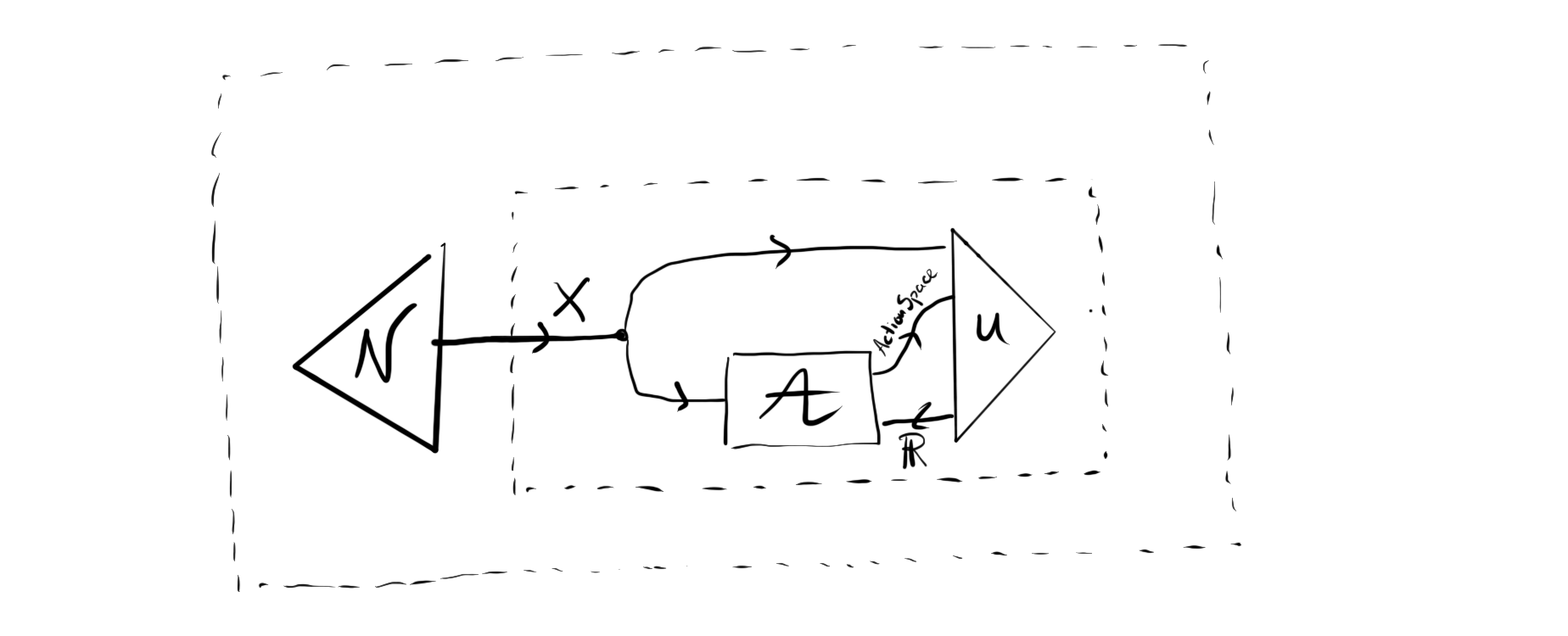
This nesting of games really shows the machinery of compositional game theory, even in these ‘trivial’ examples.
Sequential Moves
All three sequential games share the same compositional structure, they only differ in their payoff/utility functions. For example:
ultimatumGame pie = [opengame|
inputs : ;
feedback : ;
:----------------------------:
inputs : ;
feedback : ;
operation : dependentDecision "proposer" (const [1..pie]);
outputs : proposal ;
returns : ultimatumGamePayoffProposer pie proposal reaction;
inputs : proposal ;
feedback : ;
operation : dependentDecision "responder" (const [Accept,Reject]);
outputs : reaction ;
returns : ultimatumGamePayoffResponder pie proposal reaction ;
:----------------------------:
outputs : ;
returns : ;
|]
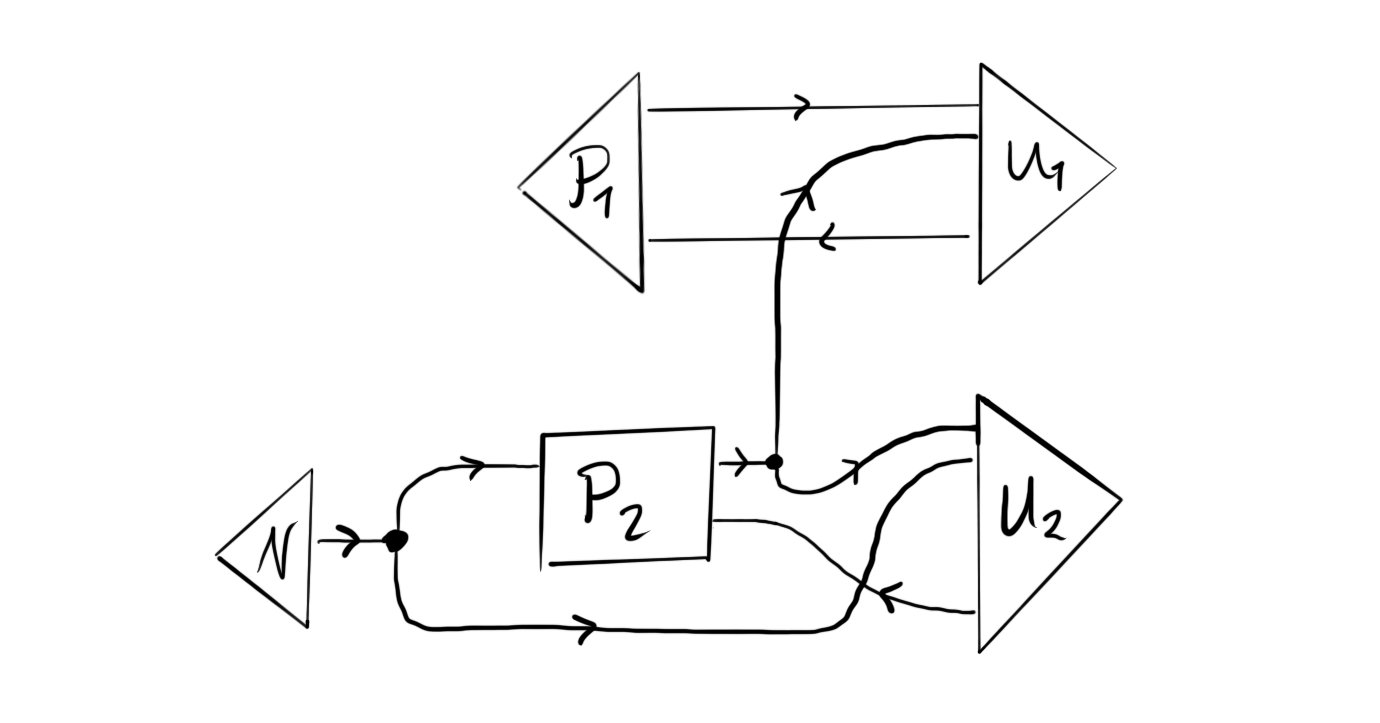
The only confusing thing is that I would write the structure as:
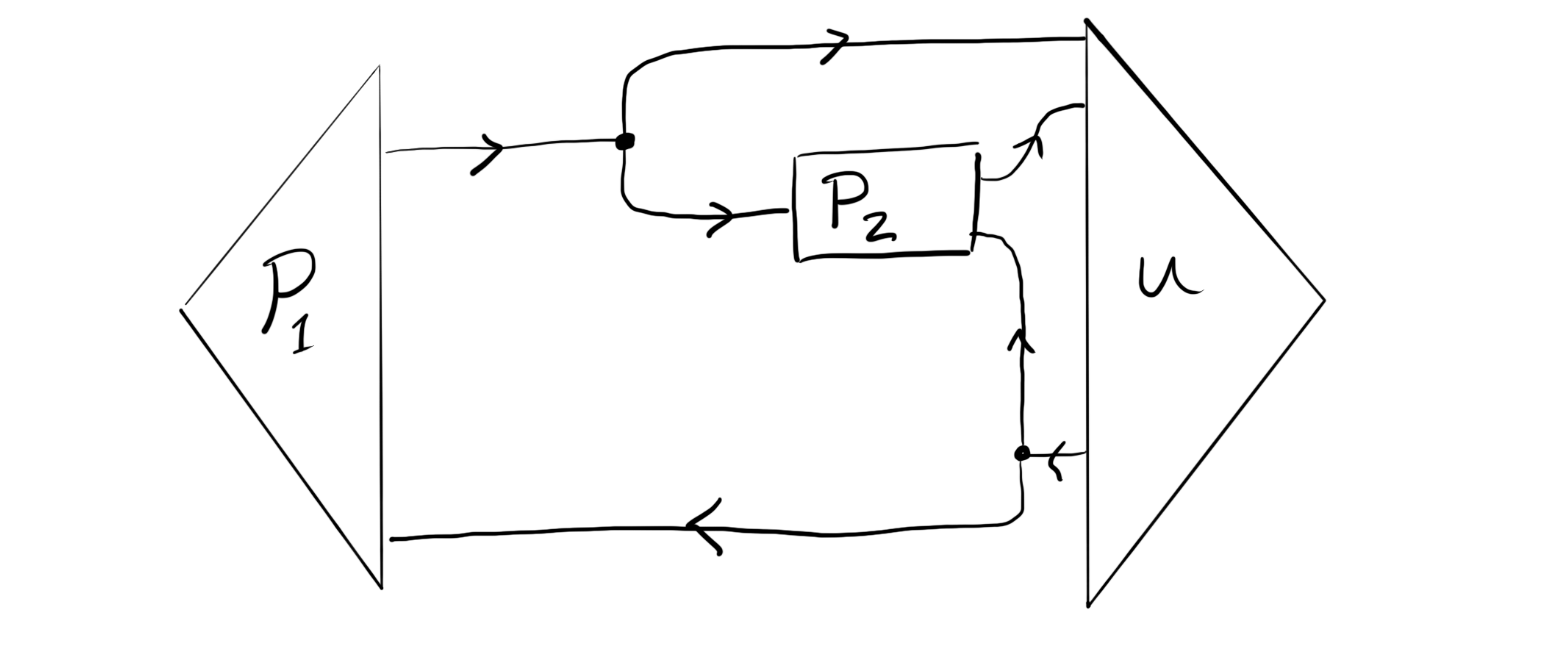
whereas the tutorial seems to represent it as
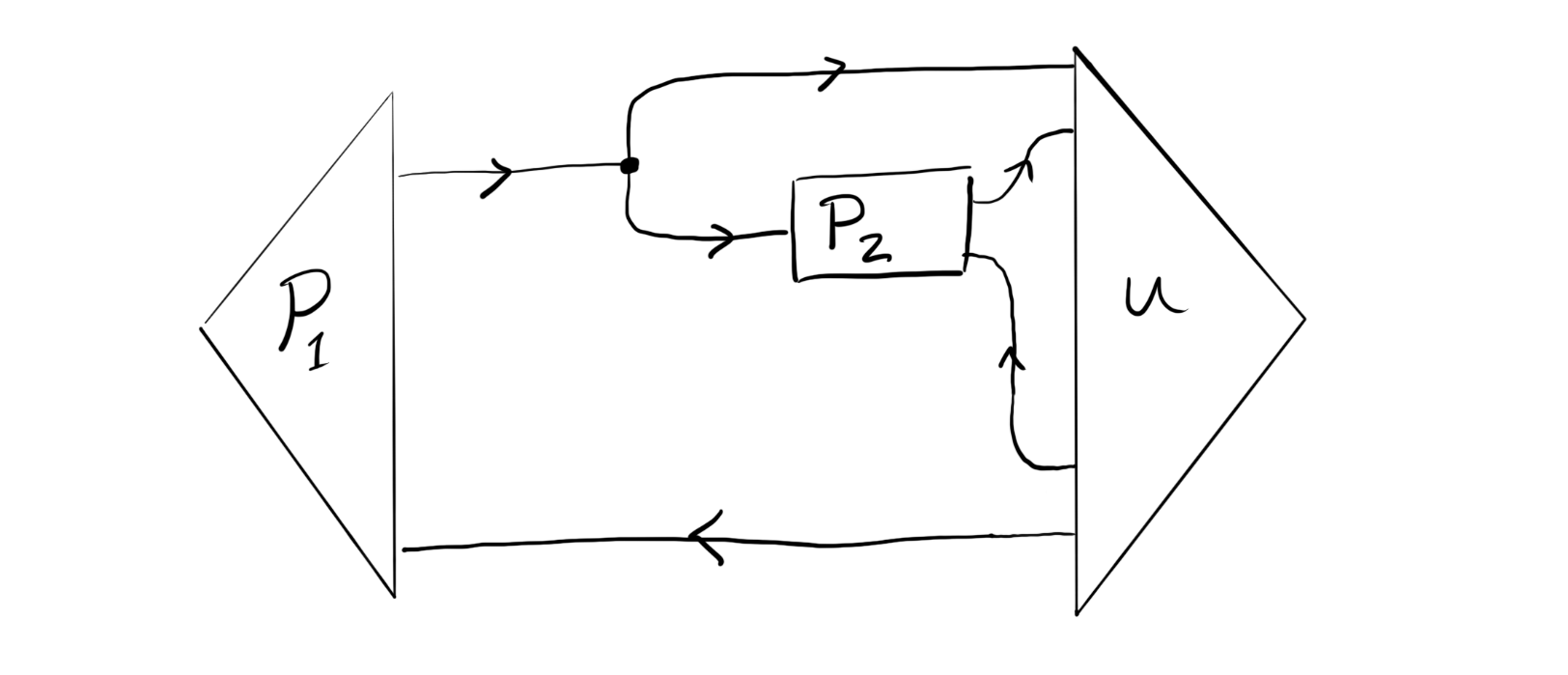
These are two slightly different situations, if I understand correctly. In the first case, both players get the full output of the utility function. In the second case, each player only gets their own utility. This seems to be a difference in information access, or are these two equivalent because all players have access to all information?
Simultaneous Moves
This class is not very interesting to convert to string diagrams, as they are all equivalent to the standard prisoner’s dilemma—they are all bimatrix games:
prisonersDilemmaReduced = [opengame|
operation : dependentDecision "player1" (const [Cooperate,Defect]);
outputs : decisionPlayer1 ;
returns : prisonersDilemmaMatrix decisionPlayer1 decisionPlayer2 ;
operation : dependentDecision "player2" (const [Cooperate,Defect]);
outputs : decisionPlayer2 ;
returns : prisonersDilemmaMatrix decisionPlayer2 decisionPlayer1 ;
|]
Since the players move at the same time, there is no way for them to observe each other, as is possible for sequential move games.

Bayesian Games
Bayesian stochasticEnv
The first Bayesian game describes how a random draw by Nature is propagated as a noisy signal:
stochasticEnv probA signalPrecision = [opengame|
inputs : ;
feedback : ;
:----------------------------:
inputs : ;
feedback : ;
operation : nature (distributionNature probA);
outputs : draw ;
returns : ;
inputs : draw ;
feedback : ;
operation : liftStochasticForward (signal signalPrecision);
outputs : signalDraw ;
returns : ;
:----------------------------:
outputs : (signalDraw,draw) ;
returns : ;
|]
which has the structure
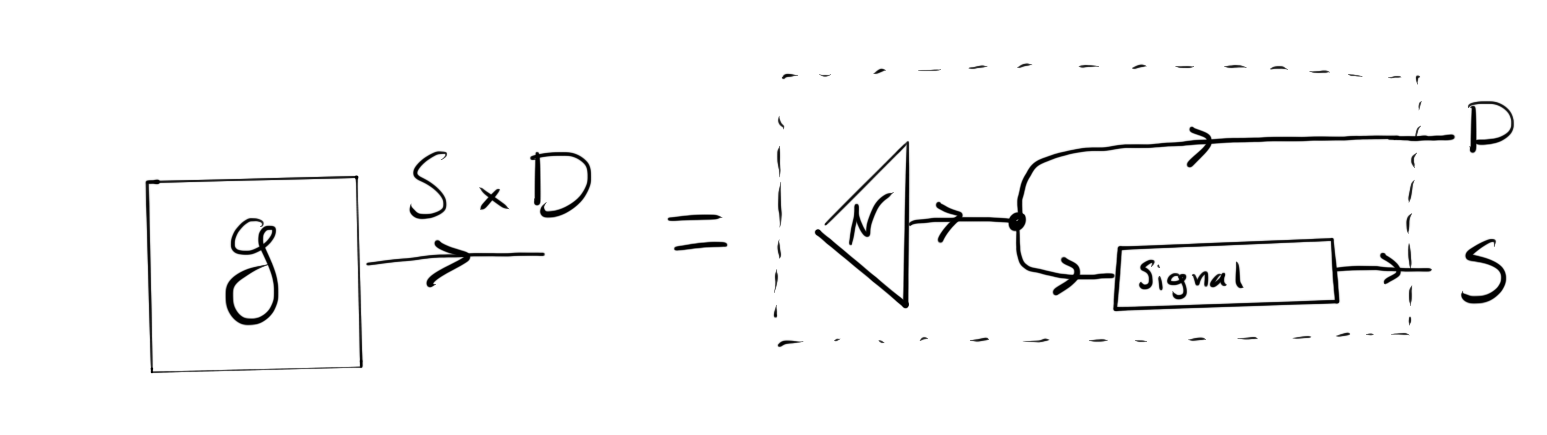
Note that this notation depends on the monoidal product $S \otimes D$ being cartesian.
CoordinateWithNature
The game Bayesian stochasticEnv is then used to send a signal to a player who makes a decision based on his belief about the original draw:
coordinateWithNature probA signalPrecision = [opengame|
inputs : ;
feedback : ;
:----------------------------:
inputs : ;
feedback : ;
operation : stochasticEnv probA signalPrecision ;
outputs : (signal,draw) ;
returns : ;
inputs : signal ;
feedback : ;
operation : dependentDecision "player" (const [A,B]);
outputs : decision ;
returns : coordinateWithNaturePayoff decision draw;
:----------------------------:
outputs : ;
returns : ;
|]
Drawn as
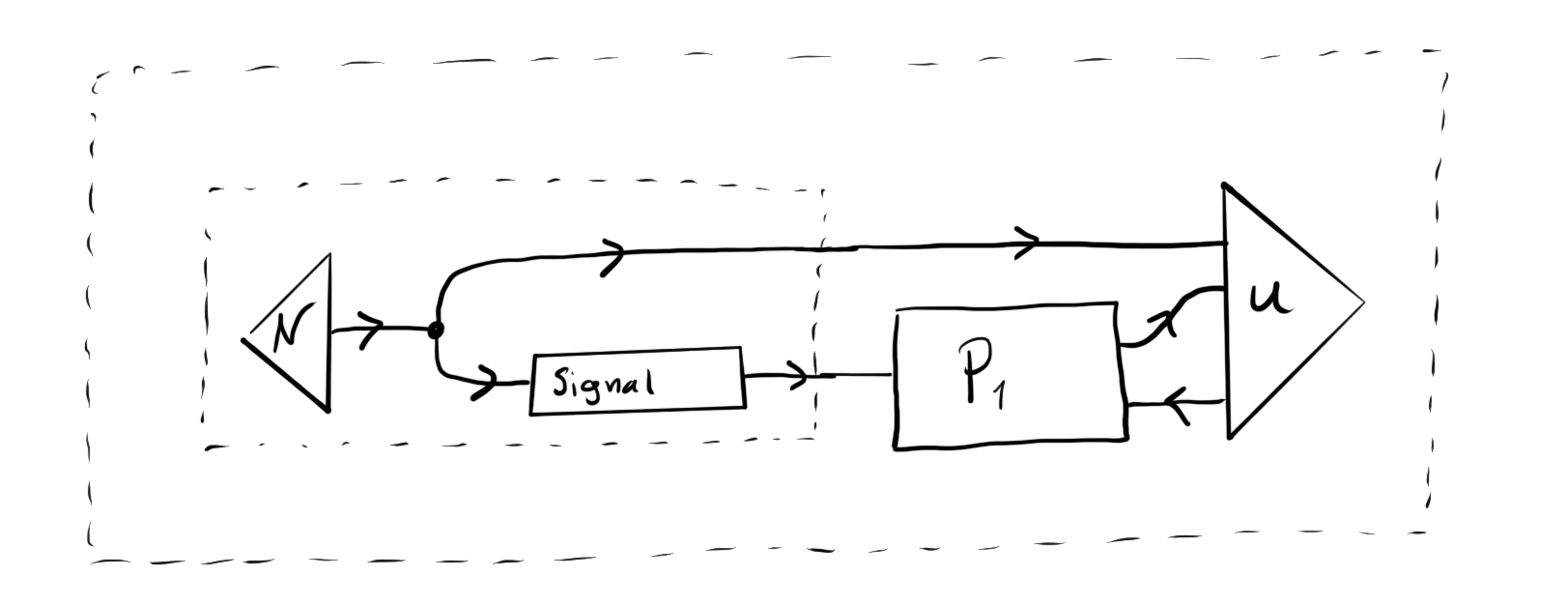
bayesianPD
Finally, a Bayesian prisoner’s dilemma is implemented as
bayesianPD = [opengame|
inputs : ;
feedback : ;
:----------------------------:
inputs : ;
feedback : ;
operation : nature (uniformDist [Rat, NoRat]) ;
outputs : prisoner2Type ;
returns : ;
inputs : ;
feedback : ;
operation : dependentDecision "prisoner1" (const [Confess, DontConfess]);
outputs : decision1 ;
returns : pdPayoff1 decision1 decision2;
inputs : prisoner2Type ;
feedback : ;
operation : dependentDecision "prisoner2" (const [Confess, DontConfess]);
outputs : decision2 ;
returns : pdPayoff2 prisoner2Type decision1 decision2 ;
:----------------------------:
outputs : ;
returns : ;
|]
That is, prisoner 2 gets assigned a type on which his payoff, and thus his behaviour depends.
maths category-theory cybernetics game-theory