Compositionally sharing pie
(This is an update on my Ethereum Protocol Fellowship. More updates can be found here ).
I wanted to make the pie sharing game compositional so that I could model an arbitrary number of players sharing the pie. I already had the 2-player game, so ‘opening up’ that game would be a logical first attempt. That would create an open game with two players, Player 1 offering a cut pie to Player 2, and Player 2 choosing one of the pieces (or equivalently: Player 1 offering a piece of the pie, and Player 2 deciding to either accept the offered piece, of choose the rest of the pie). This could be opened up by letting Player 1 start with an offered piece of pie, instead of the full pie, and choosing to accept it or not, before confronting Player 2 with the same choice, based on a cut from the piece Player 1 chose. This looks something like this:
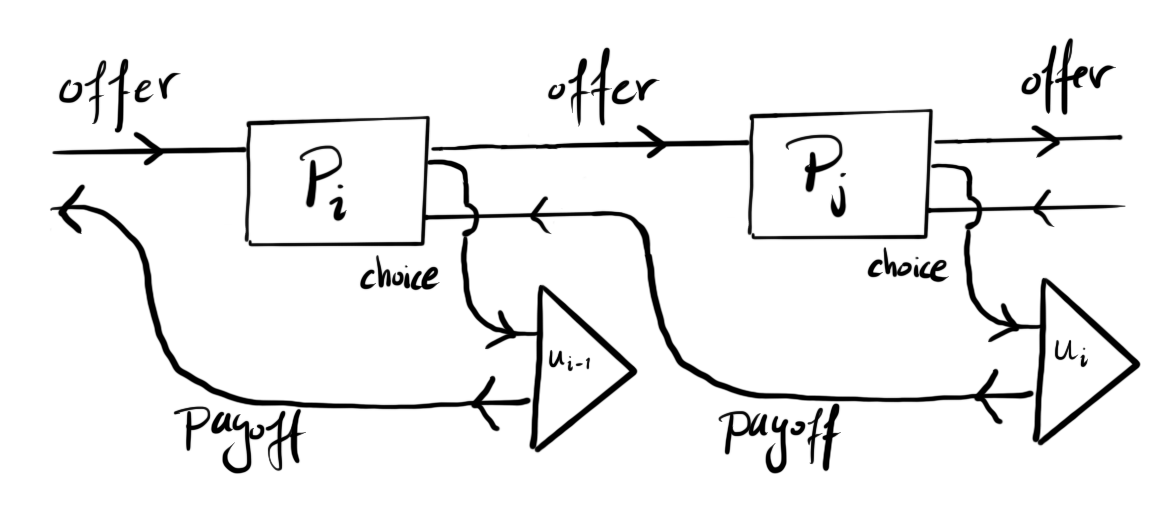
However, since each player is on equal footing, it does not really make sense to have the fundamental game be a 2-player game of two identical players. In fact, the reason I like this setup is because this game very naturally fills all arrows of an open game. Each player is confronted with an offer, responds with a choice that serves as feedback to the previous player (and determines that previous player’s payoff), and presents an offer to the next player, who will respond with similar feedback. This looks like the quintessential open game:
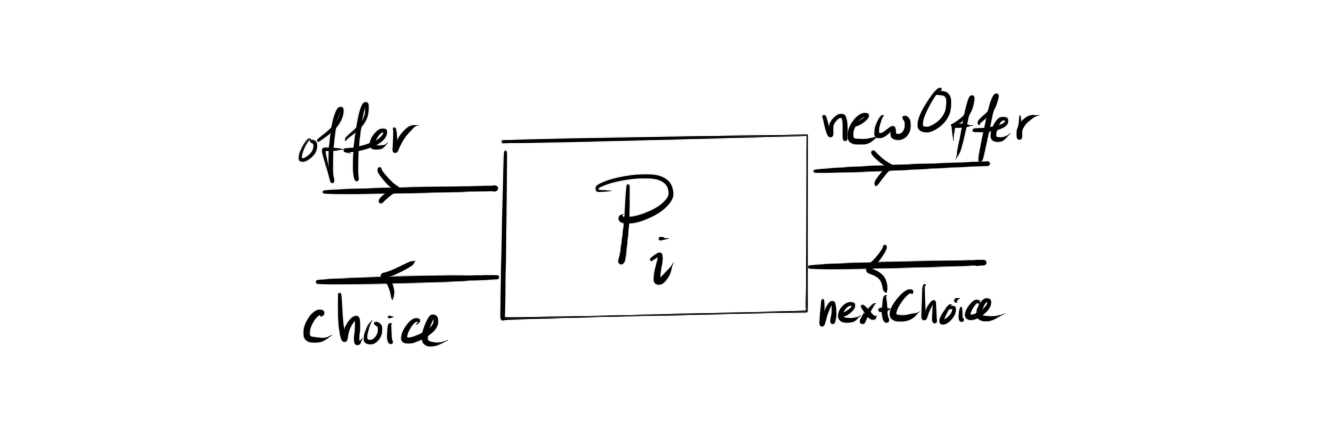
While this might be a natural way to implement this game, it relies on a dependent decision that send part of the decision (the response) to the feedback channel, and part of the decision (the new offer) to the output. This is practically hard to model. Instead, I zoomed in even more, and realised that each player actually performs two separate actions: responding to the previous player’s offer, and presenting a new offer. This can be separated, to create a situation like this, in which there are two different fundamental games:
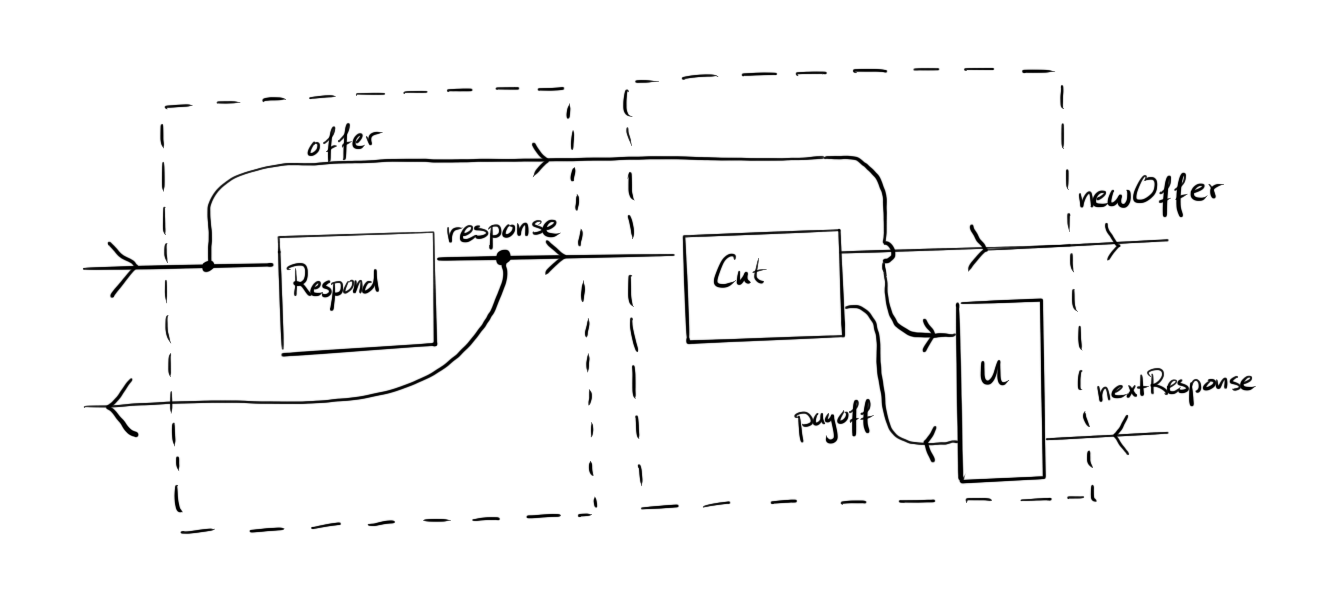
This last option has the drawback that it uses two different fundamental games, but this also allows us to change either game independently. Furthermore, the ‘Respond’ game has implicit feedback by using the cup, but no return, and the ‘Cut’ game has a return, but no feedback. This makes both much simpler decision games.
To implement this compositional structure, I first defined the relevant types and the payoff function. I chose to encode an offer as a tuple of two doubles corresponding to the sizes of the two pieces of pie after the cut. Each individual piece will just be a double, and the binary choice between the two pieces is encoded as either Accept—corresponding to choosing the first piece—or Reject, which picks the second piece. The payoff is simply the size of the final piece of pie a player ends up with:
type Offer = (Double, Double)
data ResponderAction = Accept | Reject
deriving (Eq,Ord,Show)
openPieSharingGamePayoff :: Offer -> ResponderAction -> Payoff
openPieSharingGamePayoff newOffer nextResponse =
if nextResponse == Accept then (snd newOffer) else (fst newOffer)
The ‘Respond’ game is then implemented as the following:
respondToOffer playerName = [opengame|
inputs : offer ;
feedback : response;
:----------------------------:
inputs : offer ;
feedback : ;
operation : dependentDecision playerName (const [Accept,Reject]) ;
outputs : response ;
returns : 0;
// Postpone payoff calculation, so here just return a payoff of 0.
:----------------------------:
outputs : offer, response ;
returns : ;
|]
And the ‘Cut’ game that offers a new slice to the next player is defined below, as are two helper functions that are lifted to games.
propagateChosenPiece :: Offer -> ResponderAction -> Double
propagateChosenPiece offer response = if response == Accept then (fst offer) else (snd offer)
fromOfferedPieceToOffer :: Double -> Double -> Offer
fromOfferedPieceToOffer chosenPiece offeredPiece = (offeredPiece, chosenPiece - offeredPiece)
offerNewSlice playerName = [opengame|
inputs : offer, response ;
feedback : ;
:----------------------------:
inputs : offer, response ;
feedback : ;
operation : forwardFunction $ uncurry propagateChosenPiece;
outputs : chosenPiece ;
returns : ;
inputs : chosenPiece ;
feedback : ;
operation : dependentDecision playerName actionSpace ;
outputs : newOfferedPiece ;
returns : openPieSharingGamePayoff (newOfferedPiece, chosenPiece- newOfferedPiece) newResponse;
inputs : chosenPiece, newOfferedPiece ;
feedback : ;
operation : forwardFunction $ uncurry fromOfferedPieceToOffer;
outputs : newOffer ;
returns : ;
:----------------------------:
outputs : newOffer ;
returns : newResponse;
|]
where
actionSpace x = [0, 0.1 .. x]
The two are then composed into the fundamental unit of the compositional pie sharing game:
openPieSharing_unit playerName = [opengame|
inputs : inputOffer ;
feedback : inputResponse;
:----------------------------:
inputs : inputOffer ;
feedback : inputResponse;
operation : respondToOffer playerName ;
outputs : offer, response ;
returns : ;
inputs : offer, response ;
feedback : ;
operation : offerNewSlice playerName ;
outputs : newOffer ;
returns : newResponse;
:----------------------------:
outputs : newOffer ;
returns : newResponse;
|]
At this point, I had only analysed games in a trivial context (void), so to analyse this game, I created a ‘closure’ game that add (co)point games to make the full game trivial:
pieSharingModule_closure pieSize = [opengame|
inputs : ;
feedback : ;
:---------------------------:
inputs: ;
feedback: ;
operation: dependentDecision "inputState" (const lsPie);
outputs: defaultOffer;
returns: 0;
inputs : defaultOffer ;
feedback : nullResponse ;
operation : openPieSharing_unit "player1";
outputs : offer ;
returns : nextResponse;
inputs: offer;
feedback: ;
operation: dependentDecision "continuationState" (const lsAccept);
outputs: nextResponse;
returns: 0;
:----------------------------:
outputs : ;
returns : ;
|]
where
lsPie = [pieSize]
lsAccept = [Accept]
This corresponds to a context in which a pie of size pieSize is offered, and whatever the player player1 offers to its environment gets accepted. The reason that the constant action space has to be defined outside of the Open Game Engine DSL is a parser bug, described in more detail here.
However, creating such closure games is not generally a nice way to do the analysis, as covered in the FAQ.
Therefore, instead of using this closure game, I constructed a context called contextContPie for the open openPieSharing_unit game that inputs a full pie size, and always accepts the offer made by the open game:
contextContPie :: Double -> StochasticStatefulContext
Offer
Examples.PieCutting_open.ResponderAction
Offer
Examples.PieCutting_open.ResponderAction
contextContPie fullPieSize = StochasticStatefulContext (pure ((),(fullPieSize, 0))) (\_ _ -> pure Accept)
In this context, a strategy strat can be analysed using the following functions:
evalOpenPie strat = evaluate (openPieSharing_unit "p1") strat (contextContPie 10)
isEquilibriumPieSharingGameOpen strat = generateIsEq $ evalOpenPie strat
Finally, we need to provide the actual strategies a player can have. Note that this is a single player that needs to make two different decisions: which piece to pick, and what to offer the next player. I’m not actually sure how to best implement such a dual strategy. However, the necessary type can be seen by running the following:
λ: :t isEquilibriumPieSharingGameOpen
isEquilibriumPieSharingGameOpen
:: List
'[Kleisli
Stochastic Offer ResponderAction,
Kleisli Stochastic Double Double]
-> IO ()
Which indeed matches what one would expect: a map from an offer to a response, and from a piece of pie to an cut (which is a Double, not yet a full Offer). I constructed a strategy that always accepts the incoming offer, but only offers 20% of the available pie:
selfishStrat_PieSharingOpen :: List [Kleisli Stochastic Offer ResponderAction,
Kleisli Stochastic Double Double]
selfishStrat_PieSharingOpen = Kleisli pureAccept ::- Kleisli smallOffer ::- Nil
where
pureAccept x = playDeterministically Accept
smallOffer x = playDeterministically $ 0.2*x
This allows us to analyse the final game. The equilibrium analysis gives the expected conclusion: in a context of a pie of size 10, and that always accepts any offer that the player makes, being greedy is good—while offering 2 is already a bit stingy, it’s even better to offer nothing at all:
λ: isEquilibriumPieSharingGameOpen selfishStrat_PieSharingOpen
----Analytics begin----
Strategies are in equilibrium
NEWGAME:
Strategies are NOT in equilibrium. Consider the following profitable deviations:
Player: p1
Optimal Move: 0.0
Current Strategy: fromFreqs [(2.0,1.0)]
Optimal Payoff: 10.0
Current Payoff: 8.0
Observable State: 10.0
Unobservable State: "(((),((10.0,0.0),(10.0,0.0),Accept)),((10.0,0.0),Accept,10.0))"
--other game--
--No more information--
NEWGAME:
----Analytics end----
This open game can now very nicely be composed into bigger games by just connecting all four wires and creating a ‘ladder’ of sequentially composed open games, here done for 3 players:
openPieSharing_threePlayers = [opengame|
inputs : inputOffer ;
feedback : inputResponse;
:----------------------------:
inputs : inputOffer ;
feedback : inputResponse;
operation : openPieSharing_unit "p1" ;
outputs : newOffer1 ;
returns : newResponse1 ;
inputs : newOffer1 ;
feedback : newResponse1 ;
operation : openPieSharing_unit "p2" ;
outputs : newOffer2 ;
returns : newResponse2 ;
inputs : newOffer2 ;
feedback : newResponse2 ;
operation : openPieSharing_unit "p3" ;
outputs : newOffer3 ;
returns : newResponse3 ;
:----------------------------:
outputs : newOffer3 ;
returns : newResponse3 ;
|]
Let’s define some basic strategies and combine these into full strategy profiles for the 3-player game:
pureAccept :: Offer -> Stochastic ResponderAction
pureAccept x = playDeterministically Accept
halfAccept :: Offer -> Stochastic ResponderAction
halfAccept x = if (fst x) >= (snd x) then playDeterministically Accept else playDeterministically Reject
smallOffer :: Double -> Stochastic Double
smallOffer x = playDeterministically $ 0.2*x
halfOffer :: Double -> Stochastic Double
halfOffer x = playDeterministically $ 0.5*x
zeroOffer :: Double -> Stochastic Double
zeroOffer x = playDeterministically $ 0
strat_3p_greedyP1 = Kleisli halfAccept ::- Kleisli smallOffer ::- Kleisli halfAccept ::- Kleisli halfOffer ::- Kleisli halfAccept ::- Kleisli halfOffer ::- Nil
strat_3p_eq = Kleisli halfAccept ::- Kleisli halfOffer ::- Kleisli halfAccept ::- Kleisli halfOffer ::- Kleisli halfAccept ::- Kleisli zeroOffer ::- Nil
evalOpenPie_threePlayers strat = evaluate (openPieSharing_threePlayers) strat (contextContPie 10)
isEquilibriumPieSharingGameOpen_threePlayers strat = generateIsEq $ evalOpenPie_threePlayers strat
The first strategy profile corresponds to a greedy Player 1, who only offers 20% of their cake to the next player, whereas all other players only keep half of their piece to themselves. This does not end well for Player 1, who would be much better off offering exactly half of the pie:
λ: isEquilibriumPieSharingGameOpen_threePlayers strat_3p_greedyP1
----Analytics begin----
Strategies are in equilibrium
NEWGAME:
Strategies are NOT in equilibrium. Consider the following profitable deviations:
Player: p1
Optimal Move: 5.0
Current Strategy: fromFreqs [(2.0,1.0)]
Optimal Payoff: 5.0
Current Payoff: 2.0
Observable State: 10.0
Unobservable State: "((((),(10.0,0.0)),((10.0,0.0),(10.0,0.0),Accept)),((10.0,0.0),Accept,10.0))"
--other game--
--No more information--
NEWGAME:
Strategies are in equilibrium
NEWGAME:
Strategies are in equilibrium
NEWGAME:
Strategies are in equilibrium
NEWGAME:
Strategies are NOT in equilibrium. Consider the following profitable deviations:
Player: p3
Optimal Move: 0.0
Current Strategy: fromFreqs [(2.0,1.0)]
Optimal Payoff: 4.0
Current Payoff: 2.0
Observable State: 4.0
Unobservable State: "((((),((10.0,0.0),(2.0,8.0),(4.0,4.0))),((4.0,4.0),(4.0,4.0),Accept)),((4.0,4.0),Accept,4.0))"
--other game--
--No more information--
NEWGAME:
----Analytics end----
However, the engine also shows a profitable deviation for Player 3. Currently, Player 3 offers half of their cake to the next player (the open boundary), but I defined the context to be always accepting, so Player 3 would be better off keeping everything to themselves. Making Player 1 play fairly, and Player 3 keep their piece to themselves indeed gives an equilibrium:
λ: isEquilibriumPieSharingGameOpen_threePlayers strat_3p_eq
----Analytics begin----
Strategies are in equilibrium
NEWGAME:
Strategies are in equilibrium
NEWGAME:
Strategies are in equilibrium
NEWGAME:
Strategies are in equilibrium
NEWGAME:
Strategies are in equilibrium
NEWGAME:
Strategies are in equilibrium
NEWGAME:
----Analytics end----
This can now be very easily extended to more players or different contexts. However, in each case, the equilibrium will be the strategy profile where each player chooses the biggest piece and offers half of their piece to the next player, except for the last player who can get away with offering nothing to the open boundary. That means that Player $n$ will end up with $2^{-n}$ of the original pie, except for the last player, who ends up with $2^{-(n-1)}$. That is not very fair. In fact, it’s exponentially unfair so has an asymptotic Gini coefficient of 0.5—about as unfair as the worst national income inequalities in the world. Therefore, I want to add an extra rule to this game that decides which player next shares their cake, called the BigPlayer rule, introduced here. This should make the final pie distribution fair again, and will be the subject of a next blog post.
maths category-theory game-theory