Generative models, in particular energy-based models, are often used to sample from conditional distributions–a process known as inpainting. One of the most fundamental kinds of generative energy-based models is called a restricted Boltzmann machine (RBM), which is essentially a bipartite, glassy Ising model. Inpainting with RBMs is usually done by sampling from the visible layer while fixing the value of some visible nodes, which is an intervention, not a passive observation. I could not find a proof that the resulting interventional sampling distribution approaches the conditional distribution, so here follows an argument that it in fact does (in the case of Gibbs sampling), based on the do-calculus.


Given a Bayesian network of variables $V$ represented by a DAG $G = (V, E)$, the fundamental problem in causal inference is to estimate quantities like $p_G\left(V_A=v_a \mid do(V_B=v_b)\right)$ for an arbitrary partition of the vertices $V = V_A \cup V_B$. The do-calculus provides rules and methods for answering such questions. Unfortunately, the standard formulation of RBMs is not suitable for treatment by the do-calculus, as the network of dependencies does not form a DAG. However, by exploiting the sequential nature of Gibbs-sampling, I show the following:


Lemma (RBM inpainting is conditional sampling) Consider a restricted Boltzmann machine with visible nodes $v$ and hidden nodes $h$, where $|v|>0$ and $|h|>0$. Let $p(v)$ be the marginal probability distribution over the visible nodes, and $v = v_a \cup v_b$ an arbitrary partition of the visible nodes. Consider the nodes of the RBM as random variables that evolve under alternating Gibbs sampling of the visible and the hidden layers. Define the do-operator on a variable $X$ as fixing that variable $X=x$ before generating each sample, and the see-operator as passively observing $X=x$. Then:

\[p(v_a | do(v_b)) = p(v_a | see(v_b)) = p(v_a | v_b)~~~~~~~~~~~~~~~~ (1)\]

That is, inpainting is sampling from the conditional distribution.

(proof) First note that the RBM has to be represented by a DAG. To do this, consider the nodes as random variables that evolve under Gibbs sampling. The bipartite structure of the network allows us to unroll the network in time:



where $v^i$ and $h^i$ mark the $i$’th Gibbs sample of the visible and hidden layer, respectively. Given the partition $v = v_a \cup v_b$, the following should be verified:

\[p(v^1_a \mid do(v^0_b)) = p(v^1_a \mid v^0_b) ~~~~~~~~~~~~~~~~ (2)\]

The second rule of the do-calculus states:


Rule 2(Action/observation exchange)

\[p(y \mid do(x), do(z), w) = p(y \mid do(x), z, w) \text{ if } (Y\!\perp\!\!\!\perp Z \mid X, W)_{G_{\overline{X}\underline{Z}}}\]

where $G_{\overline{X}\underline{Z}}$ is the graph $G$ with all the arrows into $X$, and out of $Z$ removed. If $X=W=\emptyset$, then Rule 2 can be directly apply to Equation (1) by defining the following two graphs:



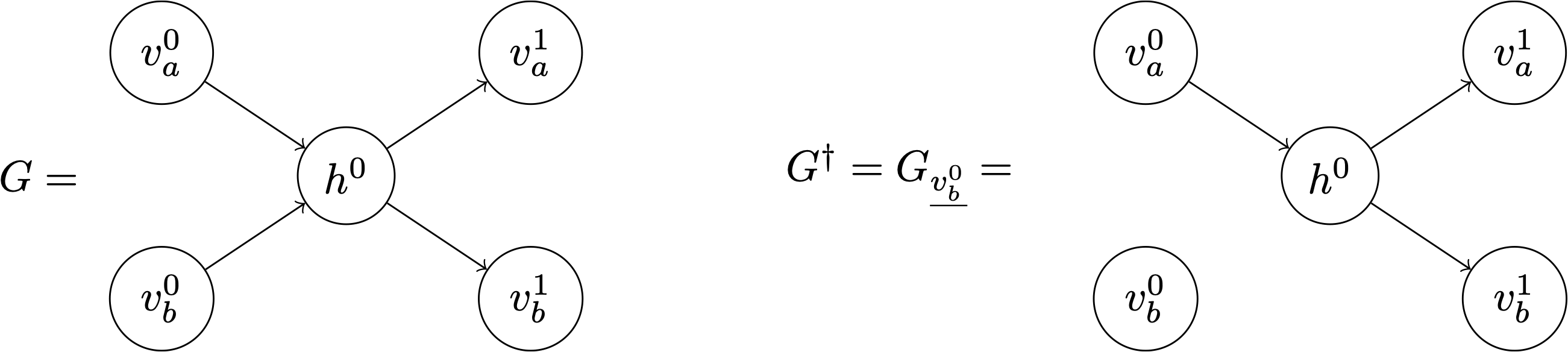
where $v$ could be partitioned because at any given time point the visible nodes are mutually independent conditional on the hidden layer. The value of $v_b^1$ will be discarded and set to $v_b^0$ again, but that is irrelevant in the present discussion. Now \((v_a^1 \!\perp\!\!\!\perp v_b^0)_{G^\dagger}\), which by Rule 2 implies Equation (2), and completes the proof. $\square$



Example As a very simple example, consider the case where $v_a=v_1$, $v_b=v_2$ and $h_1$ all comprise just a single node. The full distribution is:

\[P_G(v_1, v_2, h_1) = \frac{1}{\mathcal{Z}_G} e^{h_1 w_{11} v_1 + h_1 w_{12} v_2 + b_1 v_1 + b_2 v_2 + c_1 h_i}\]

Denoting by $(abc)$ the situation in which $v_1=a, ~v_2=b, ~h_1=c$, the conditional distribution after observing $v_2=1$ is:


\[\begin{align*} P(v_1=1|\text{see}(v_2=1)) &= \frac{P_G(v_1=1, v_2=1)}{P_G(v_2=1)}\\ &= \frac{(110) + (111)}{(111) + (110) + (011) + (010)}\\ &= \frac{e^{b_1+b_2} + e^{w_{11} + w_{12} + b_1 + b_2 + c_1}}{e^{w_{11}+w{12}+b_1+b_2+c_1} + e^{b_1+b_2} + e^{w_{12} + b_2 + c_1} + e^{b_2}}\\ &= \frac{e^{b_1} + e^{w_{11} + w_{12} + b_1 + c_1}}{e^{w_{11}+w{12}+b_1+c_1} + e^{b_1} + e^{w_{12} + c_1} + 1} \end{align*}\]


Now consider the intervention $do(v_2=1)$. It just adds a bias $w_{12}$ to the hidden layer. Denoting by $(ab)$ that $v_1=a, ~h_1=b$:


\[\begin{align*} P_G(v_1=1|\text{do}(v_2=1)) &= P_{G^\dagger}(v_1=1)\\ &= \frac{1}{\mathcal{Z}_{G^\dagger}} \Big((11) + (10)\Big) \end{align*}\]


Writing out this partition function:


\[\mathcal{Z}_{G^\dagger} = (11) + (10) + (01) + (00) = e^{w_{11}+b_1+c_1+w_{12}} + e^{b_1} + e^{c_1+w_{12}} + 1\]


so that


\[P(v_1=1|\text{do}(v_2=1)) = \frac{e^{w_{11}+b_1+c_1+w_{12}} + e^{b_1}}{e^{w_{11}+b_1+c_1+w_{12}} + e^{b_1} + e^{c_1+w_{12}} + 1}\]

which indeed coincides with expression for the see-operator.